这篇教程python numpy中multiply与*及matul 的区别说明写得很实用,希望能帮到您。
1、对于矩阵(matrix)而言multiply是对应元素相乘,而 * 、np.matmul() 函数 与 np.dot()函数 相当于矩阵乘法(矢量积),对应的列数和行数必须满足乘法规则;如果希望以数量积的方式进行,则必须使用 np.multiply 函数,如下所示: a = np.mat([[1, 2, 3, 4, 5]])b = np.mat([[1,2,3,4,5]])c=np.multiply(a,b)print(c) 结果是 [[ 1 4 9 16 25]]
a = np.mat([[1, 2, 3, 4, 5]])
b = np.mat([ [1],[2],[3],[4],[5] ] )
d=a*b
print(d) #a是shape(1,5),b是shape(5,1),结果是一个实数
结果是 [[55]]
2、对于数组(Array)而言* 与 multiply均表示的是数量积(即对应元素的乘积相加),np.matmul与np.dot表示的是矢量积(即矩阵乘法)。 代码: if __name__ == '__main__': w = np.array([[1,2],[3,4]]) x = np.array([[1,3],[2,4]]) w1 = np.array([[1,2],[3,4]]) x1 = np.array([[1,2]]) w_mat = np.mat([[1,2],[3,4]]) x_mat = np.mat([[1,3],[2,4]]) print("x1.shape:",np.shape(x1)) w_x_start = w*x w_x_dot = np.dot(w,x) x_w_dot = np.dot(x,w) w_x_matmul = np.matmul(w, x) x_w_matmul = np.matmul(x, w) w_x_multiply = np.multiply(w,x) x_w_multiply = np.multiply(x, w) #w1_x1_matmul = np.matmul(w1, x1) x1_w1_matmul = np.matmul(x1, w1) w_x_mat_matmul = np.matmul(w_mat,x_mat) x_w_mat_matmul = np.matmul(x_mat, w_mat) w_x_mat_start = w_mat*x_mat x_w_mat_start = x_mat*w_mat w_x_mat_dot = np.dot(w_mat,x_mat) x_w_mat_dot = np.dot(x_mat,w_mat) w_x_mat_multiply = np.multiply(w_mat,x_mat) x_w_mat_multiply = np.multiply(x_mat,w_mat) print("W.shape:", np.shape(w)) print("x.shape:", np.shape(x)) print("w_x_start.shape:", np.shape(w_x_start)) print("w_x_dot.shape:", np.shape(w_x_dot)) print("x_w_dot.shape:", np.shape(x_w_dot)) print("x1_w1_matmul.shape::", np.shape(x1_w1_matmul)) print("做Array数组运算时:", '/n') print("w_x_start:", w_x_start) print("w_x_dot:", w_x_dot) print("x_w_dot:", x_w_dot) print("w_x_matmul:", w_x_matmul) print("x_w_matmul:", x_w_matmul) print("w_x_multiply:", w_x_multiply) print("x_w_multiply:", x_w_multiply) # print("w1_x1_matmul:", w1_x1_matmul) print("x1_w1_matmul:", x1_w1_matmul) print("做matrix矩阵运算时:", '/n') print("w_x_mat_start:", w_x_mat_start) print("x_w_mat_start:", x_w_mat_start) print("x_w_mat_dot:", x_w_mat_dot) print("w_x_mat_dot:", w_x_mat_dot) print("w_x_mat_matmul:",w_x_mat_matmul) print("x_w_mat_matmul:", x_w_mat_matmul) print("w_x_mat_multiply",w_x_mat_multiply) print("x_w_mat_multiply", x_w_mat_multiply)x1.shape: (1, 2)W.shape: (2, 2)x.shape: (2, 2)w_x_start.shape: (2, 2)w_x_dot.shape: (2, 2)x_w_dot.shape: (2, 2)x1_w1_matmul.shape:: (1, 2)做Array数组运算时: w_x_start: [[ 1 6] [ 6 16]]w_x_dot: [[ 5 11] [11 25]]x_w_dot: [[10 14] [14 20]]w_x_matmul: [[ 5 11] [11 25]]x_w_matmul: [[10 14] [14 20]]w_x_multiply: [[ 1 6] [ 6 16]]x_w_multiply: [[ 1 6] [ 6 16]]x1_w1_matmul: [[ 7 10]]做matrix矩阵运算时: w_x_mat_start: [[ 5 11] [11 25]]x_w_mat_start: [[10 14] [14 20]]x_w_mat_dot: [[10 14] [14 20]]w_x_mat_dot: [[ 5 11] [11 25]]w_x_mat_matmul: [[ 5 11] [11 25]]x_w_mat_matmul: [[10 14] [14 20]]w_x_mat_multiply [[ 1 6] [ 6 16]]x_w_mat_multiply [[ 1 6] [ 6 16]] python中转置的优先级高于乘法运算 例如: a = np.mat([[2, 3, 4]])
b = np.mat([[1,2,3]] )
d=a*b.T
print(d)
结果是 [[20]]
其中a为1行3列,b也为1行3列,按理来说直接计算a*b是不能运算,但是计算d=a*b.T是可以的,结果是20,说明运算顺序是先转置再计算a与b转置的积,*作为矩阵乘法,值得注意的在执行*运算的时候必须符合行列原则。 numpy中tile()函数的用法b = tile(a,(m,n)):即是把a数组里面的元素复制n次放进一个数组c中,然后再把数组c复制m次放进一个数组b中,通俗地讲就是将a在行方向上复制m次,在列方向上复制n次。 python中的 sum 和 np.sum 是不一样的,如果只写sum的话,表示的是数组中对应的维度相加,如果写 np.sum 的话,表示一个数组中的维数和列数上的数都加在一起。 如下图所示: 
补充:总结:numpy中三个乘法运算multiply,dot和* 的区别 引言:本人在做机器学习的练习1的时候,时常抛出错误: 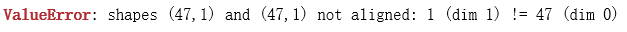
Not aligned是什么意思呢?意思是两个矩阵相乘无意义。 线性代数中mxn 和 nxp的矩阵才能相乘,其结果是mxp的矩阵。 出错源代码:def gradientDescent(X,y,theta,alpha,iteration): colunms = int(theta.ravel().shape[1]) thetai = np.matrix(np.zeros(theta.shape)) cost = np.zeros(iteration) for i in range(iteration): error = X*theta.T-y for j in range(colunms): a = np.sum(error*X[:,j])/len(X) ########## error! thetai[0,j] = thetai[0,j] - alpha*a theta = thetai cost[i] = computeCost(X, y, theta) return theta,cost 这里error是一个nx1的矩阵,theta.T也是一个nx1的矩阵。 而矩阵之间*运算符表示矩阵乘法。我们这里想实现矩阵的对应元素相乘,因此应该用np.multiply()实现。 总结:(读者可使用简单的举例自行验证) 1.*用法:矩阵与矩阵:矩阵乘法(matrix) 数组与数组:对应位置相乘(array) 2.np.dot()用法:矩阵相乘的结果 3.np.multiply()用法:数组、矩阵都得到对应位置相乘。 以上为个人经验,希望能给大家一个参考,也希望大家多多支持51zixue.net。
python文本处理的方案(结巴分词并去除符号)
tensorflow中的梯度求解及梯度裁剪操作 |

