这篇教程pytorch 中autograd.grad()函数的用法说明写得很实用,希望能帮到您。
我们在用神经网络求解PDE时, 经常要用到输出值对输入变量(不是Weights和Biases)求导; 在训练WGAN-GP 时, 也会用到网络对输入变量的求导。 以上两种需求, 均可以用pytorch 中的autograd.grad() 函数实现。 autograd.grad(outputs, inputs, grad_outputs=None, retain_graph=None, create_graph=False, only_inputs=True, allow_unused=False)
outputs: 求导的因变量(需要求导的函数)
inputs: 求导的自变量
grad_outputs: 如果 outputs为标量,则grad_outputs=None,也就是说,可以不用写; 如果outputs 是向量,则此参数必须写,不写将会报如下错误:

那么此参数究竟代表着什么呢? 先假设 为一维向量, 即可设自变量因变量分别为 为一维向量, 即可设自变量因变量分别为 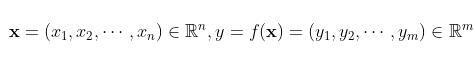 , 其对应的 Jacobi 矩阵为 , 其对应的 Jacobi 矩阵为 
grad_outputs 是一个shape 与 outputs 一致的向量, 即 
在给定grad_outputs 之后,真正返回的梯度为 
为方便下文叙述我们引入记号 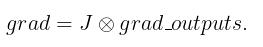 其次假设  ,第i个列向量对应的Jacobi矩阵为 ,第i个列向量对应的Jacobi矩阵为 
此时的grad_outputs 为(维度与outputs一致) 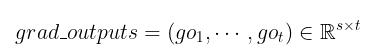
由第一种情况, 我们有 
也就是说对输出变量的列向量求导,再经过权重累加。 若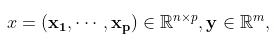 沿用第一种情况记号 沿用第一种情况记号  , 其中每一个 , 其中每一个 均由第一种方法得出, 均由第一种方法得出,
即对输入变量列向量求导,之后按照原先顺序排列即可。 retain_graph: True 则保留计算图, False则释放计算图 create_graph: 若要计算高阶导数,则必须选为True allow_unused: 允许输入变量不进入计算 下面我们看一下具体的例子: import torchfrom torch import autograd x = torch.rand(3, 4)x.requires_grad_() 观察 x 为 
不妨设 y 是 x 所有元素的和, 因为 y是标量,故计算导数不需要设置grad_outputs y = torch.sum(x)grads = autograd.grad(outputs=y, inputs=x)[0]print(grads) 结果为 
若y是向量 y = x[:,0] +x[:,1]# 设置输出权重为1grad = autograd.grad(outputs=y, inputs=x, grad_outputs=torch.ones_like(y))[0]print(grad)# 设置输出权重为0grad = autograd.grad(outputs=y, inputs=x, grad_outputs=torch.zeros_like(y))[0]print(grad) 结果为 
最后, 我们通过设置 create_graph=True 来计算二阶导数 y = x ** 2grad = autograd.grad(outputs=y, inputs=x, grad_outputs=torch.ones_like(y), create_graph=True)[0]grad2 = autograd.grad(outputs=grad, inputs=x, grad_outputs=torch.ones_like(grad))[0]print(grad2) 结果为 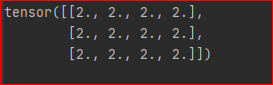
综上,我们便搞清楚了它的求导机制。 补充:pytorch学习笔记:自动微分机制(backward、torch.autograd.grad) 一、前言神经网络通常依赖反向传播求梯度来更新网络参数,求梯度过程通常是一件非常复杂而容易出错的事情。 而深度学习框架可以帮助我们自动地完成这种求梯度运算。 Pytorch一般通过反向传播 backward方法 实现这种求梯度计算。该方法求得的梯度将存在对应自变量张量的grad属性下。 除此之外,也能够调用torch.autograd.grad函数来实现求梯度计算。 这就是Pytorch的自动微分机制。 二、利用backward方法求导数backward方法通常在一个标量张量上调用,该方法求得的梯度将存在对应自变量张量的grad属性下。如果调用的张量非标量,则要传入一个和它同形状的gradient参数张量。相当于用该gradient参数张量与调用张量作向量点乘,得到的标量结果再反向传播。 1, 标量的反向传播import numpy as np import torch # f(x) = a*x**2 + b*x + c的导数x = torch.tensor(0.0,requires_grad = True) # x需要被求导a = torch.tensor(1.0)b = torch.tensor(-2.0)c = torch.tensor(1.0)y = a*torch.pow(x,2) + b*x + c y.backward()dy_dx = x.gradprint(dy_dx) 输出: tensor(-2.)
2, 非标量的反向传播import numpy as np import torch # f(x) = a*x**2 + b*x + cx = torch.tensor([[0.0,0.0],[1.0,2.0]],requires_grad = True) # x需要被求导a = torch.tensor(1.0)b = torch.tensor(-2.0)c = torch.tensor(1.0)y = a*torch.pow(x,2) + b*x + c gradient = torch.tensor([[1.0,1.0],[1.0,1.0]])print("x:/n",x)print("y:/n",y)y.backward(gradient = gradient)x_grad = x.gradprint("x_grad:/n",x_grad)输出: x: tensor([[0., 0.], [1., 2.]], requires_grad=True) y: tensor([[1., 1.], [0., 1.]], grad_fn=<AddBackward0>) x_grad: tensor([[-2., -2.], [ 0., 2.]])
3, 非标量的反向传播可以用标量的反向传播实现import numpy as np import torch # f(x) = a*x**2 + b*x + cx = torch.tensor([[0.0,0.0],[1.0,2.0]],requires_grad = True) # x需要被求导a = torch.tensor(1.0)b = torch.tensor(-2.0)c = torch.tensor(1.0)y = a*torch.pow(x,2) + b*x + c gradient = torch.tensor([[1.0,1.0],[1.0,1.0]])z = torch.sum(y*gradient)print("x:",x)print("y:",y)z.backward()x_grad = x.gradprint("x_grad:/n",x_grad)输出: x: tensor([[0., 0.], [1., 2.]], requires_grad=True) y: tensor([[1., 1.], [0., 1.]], grad_fn=<AddBackward0>) x_grad: tensor([[-2., -2.], [ 0., 2.]])
三、利用autograd.grad方法求导数import numpy as np import torch # f(x) = a*x**2 + b*x + c的导数x = torch.tensor(0.0,requires_grad = True) # x需要被求导a = torch.tensor(1.0)b = torch.tensor(-2.0)c = torch.tensor(1.0)y = a*torch.pow(x,2) + b*x + c# create_graph 设置为 True 将允许创建更高阶的导数 dy_dx = torch.autograd.grad(y,x,create_graph=True)[0]print(dy_dx.data)# 求二阶导数dy2_dx2 = torch.autograd.grad(dy_dx,x)[0] print(dy2_dx2.data) 输出: tensor(-2.) tensor(2.)
import numpy as np import torch x1 = torch.tensor(1.0,requires_grad = True) # x需要被求导x2 = torch.tensor(2.0,requires_grad = True)y1 = x1*x2y2 = x1+x2# 允许同时对多个自变量求导数(dy1_dx1,dy1_dx2) = torch.autograd.grad(outputs=y1, inputs = [x1,x2],retain_graph = True)print(dy1_dx1,dy1_dx2)# 如果有多个因变量,相当于把多个因变量的梯度结果求和(dy12_dx1,dy12_dx2) = torch.autograd.grad(outputs=[y1,y2], inputs = [x1,x2])print(dy12_dx1,dy12_dx2) 输出: tensor(2.) tensor(1.) tensor(3.) tensor(2.)
四、利用自动微分和优化器求最小值import numpy as np import torch # f(x) = a*x**2 + b*x + c的最小值x = torch.tensor(0.0,requires_grad = True) # x需要被求导a = torch.tensor(1.0)b = torch.tensor(-2.0)c = torch.tensor(1.0)optimizer = torch.optim.SGD(params=[x],lr = 0.01)def f(x): result = a*torch.pow(x,2) + b*x + c return(result)for i in range(500): optimizer.zero_grad() y = f(x) y.backward() optimizer.step() print("y=",f(x).data,";","x=",x.data)输出: y= tensor(0.) ; x= tensor(1.0000)
以上为个人经验,希望能给大家一个参考,也希望大家多多支持51zixue.net。如有错误或未考虑完全的地方,望不吝赐教。
python3实现无权最短路径的方法
python3实现Dijkstra算法最短路径的实现 |

