这篇教程Datawhale练习之二手车价格预测写得很实用,希望能帮到您。
数据探索性分析(EDA)
1. 总览数据概况数据库载入 #coding:utf-8#导入warnings包,利用过滤器来实现忽略警告语句。import warningswarnings.filterwarnings('ignore')import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snsimport missingno as msno数据载入 ## 1) 载入训练集和测试集;path = './'Train_data = pd.read_csv(path+'car_train_0110.csv', sep=' ')Test_data = pd.read_csv(path+'car_testA_0110.csv', sep=' ') 确定path,如果是在notebook环境,我通常使用 !dir查看当前目录 
特征说明 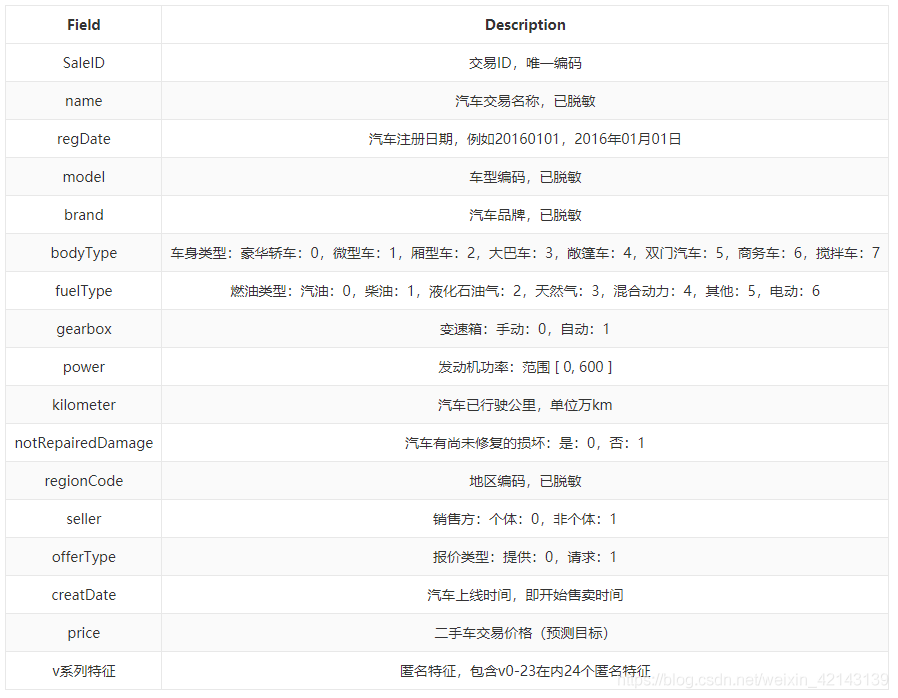
新技能:使用.append()同时观察前5行与后5行 ## 2) 简略观察数据(head()+shape)Train_data.head().append(Train_data.tail()) 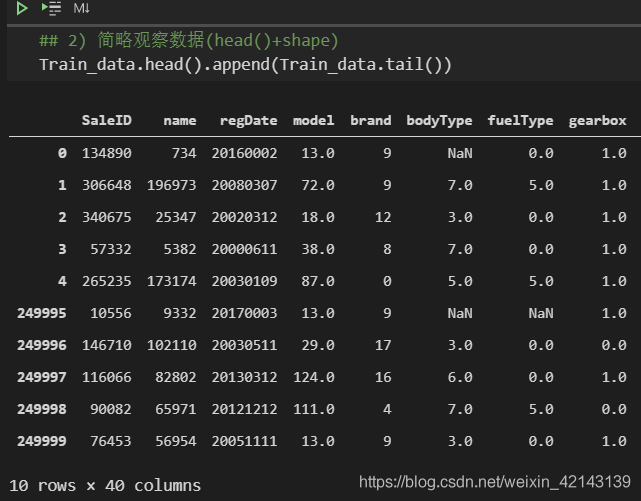
观察数据维度 Train_data.shape,Test_data.shape 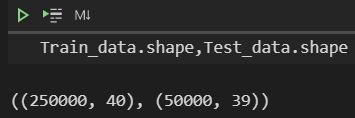
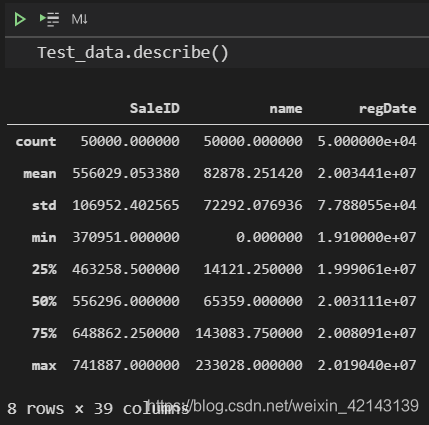
总览概况: .describe()查看统计量,.info()查看数据类型 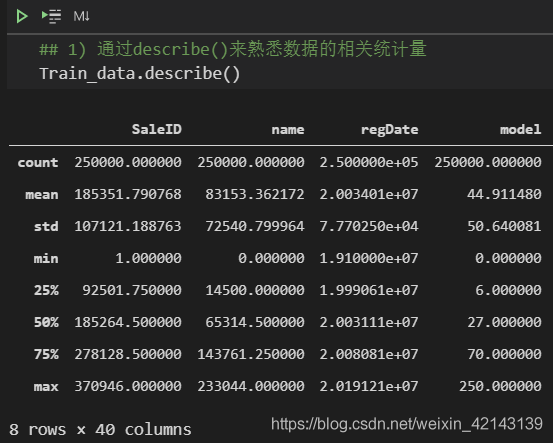
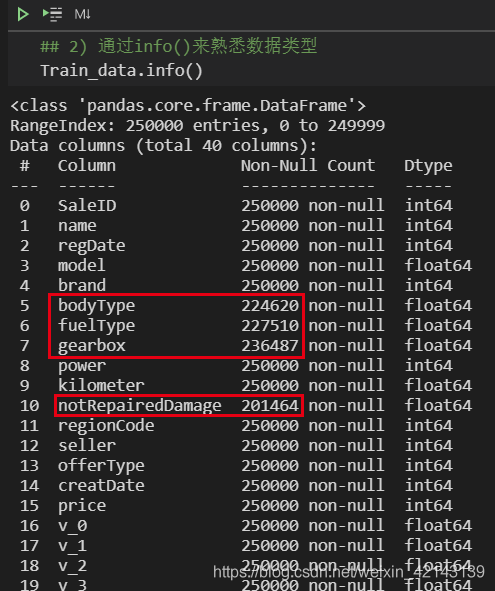
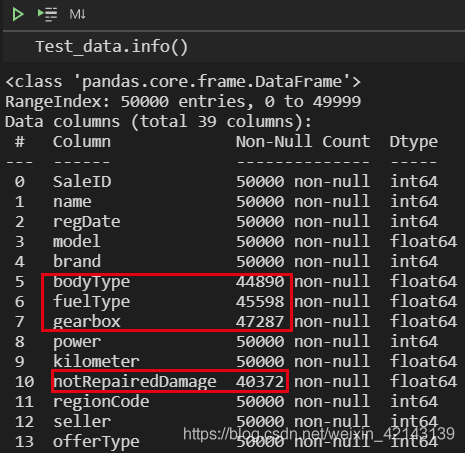
1.1 判断数据缺失和异常
1.1.1 查看nanTrain_data.shape,Test_data.shape 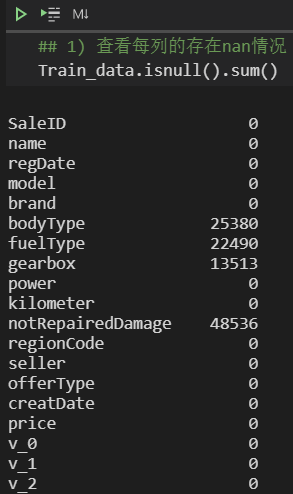
也可直接查看nan,有以下两种方式 ↓ : Train_data.isnull().sum() 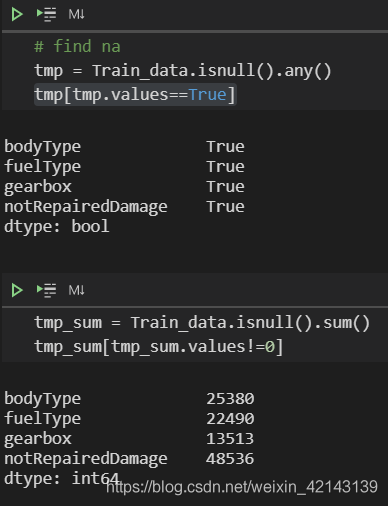
可视化na更直观 # find na tmp = df_train.isnull().any()tmp[tmp.values==True] 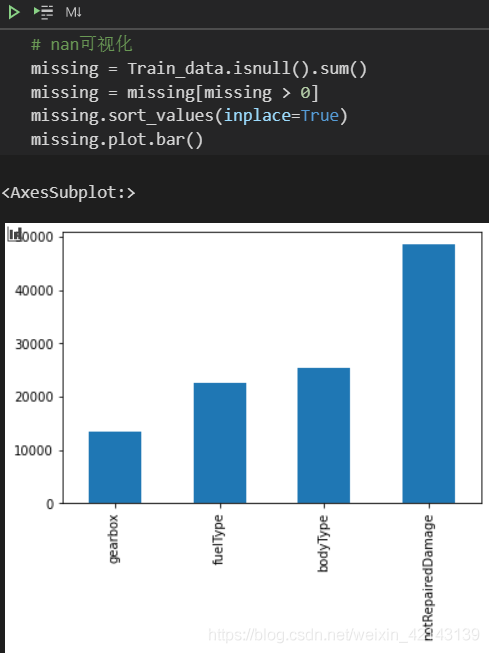
新技能: msno库(缺失值可视化)的使用 Train_data.isnull().sum().plot( kind= 'bar') 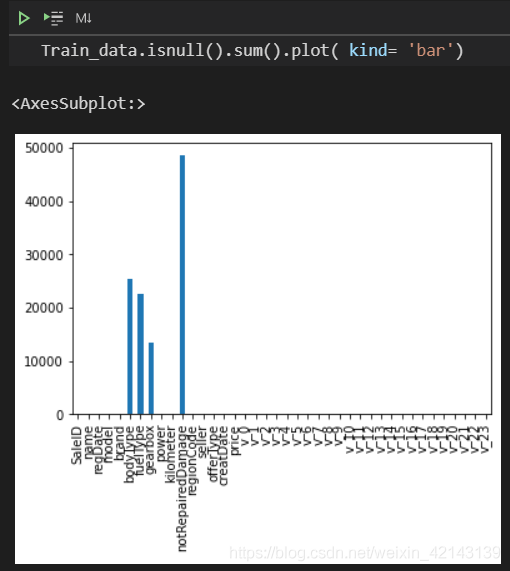
可视化看下缺省值 msno.matrix(Train_data.sample(250)) 其中,Train_data.sample(250)表示随机抽样250行,白色条纹表示缺失 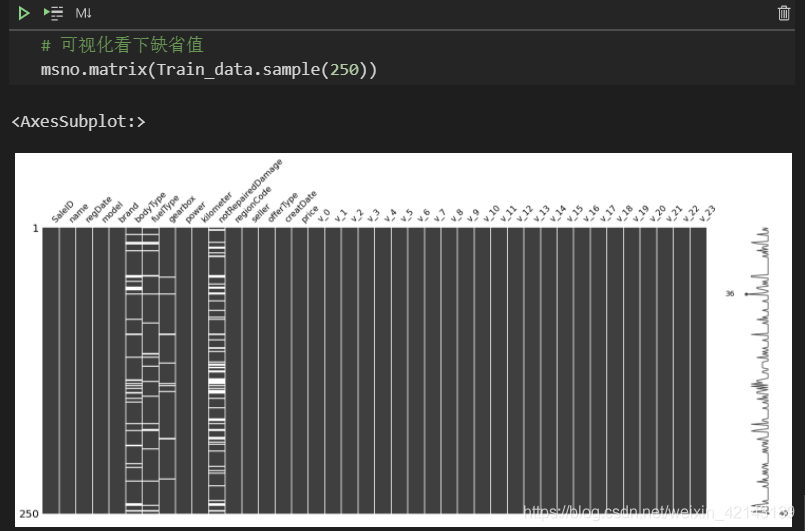
直接显示未缺失的样本数量/每特征 msno.bar(Train_data.sample(250),labels= True) 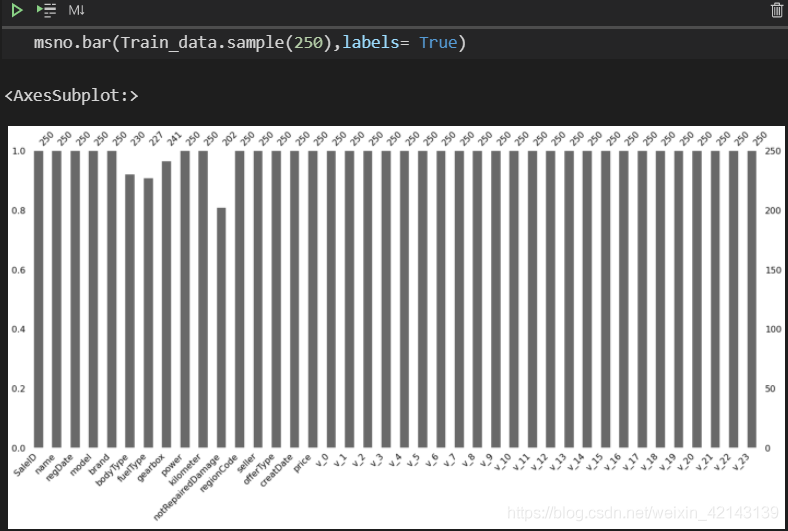
使用msno中的 .heatmap()查看缺失值之间的相关性 msno.heatmap(Train_data.sample(250)) 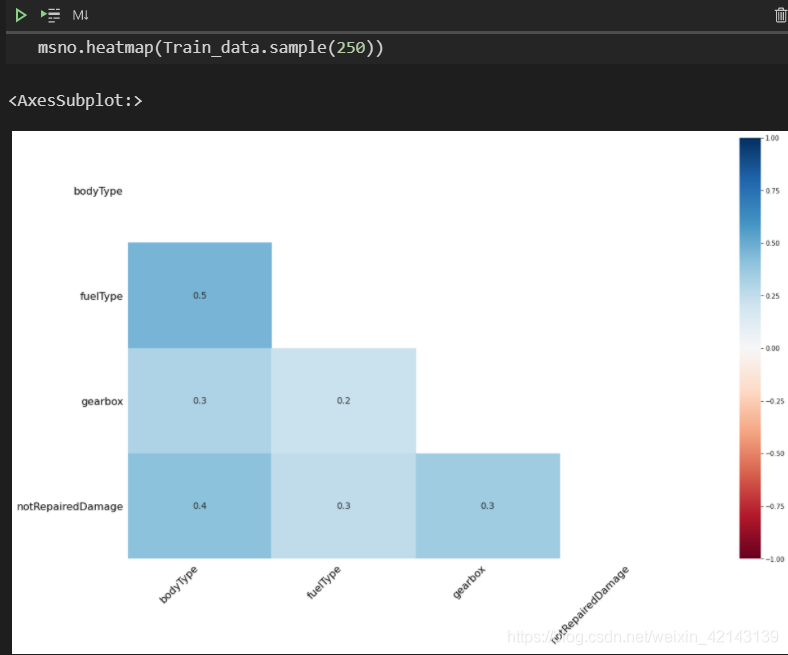
1.1.2 *异常值检测(重要!易忽略)通过Train_data.info()了解数据类型
1.2 了解预测值的分布查看分布的意义在于: a. 及时将非正态分布数据变化为正态分布数据 b. 异常检测
1.2.1 数字特征分析发现都是int 
统计分布 ↓ Train_data['price'].value_counts() 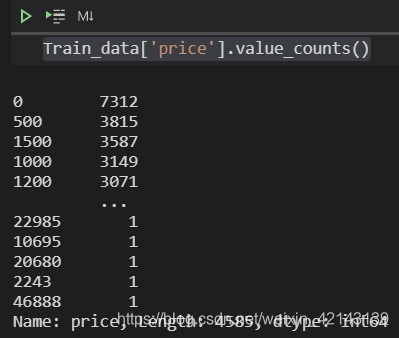
## 1) 总体分布概况(无界约翰逊分布等)import scipy.stats as sty = Train_data['price']plt.figure(1); plt.title('Johnson SU')sns.distplot(y, kde=False, fit=st.johnsonsu)plt.figure(2); plt.title('Normal')sns.distplot(y, kde=False, fit=st.norm)plt.figure(3); plt.title('Log Normal')sns.distplot(y, kde=False, fit=st.lognorm)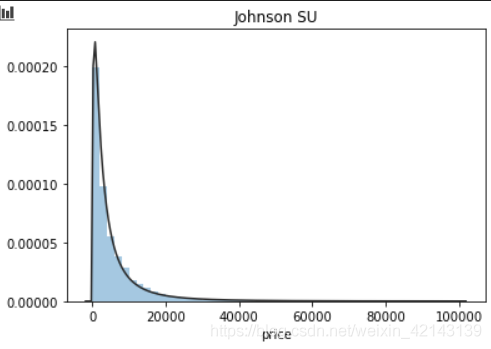
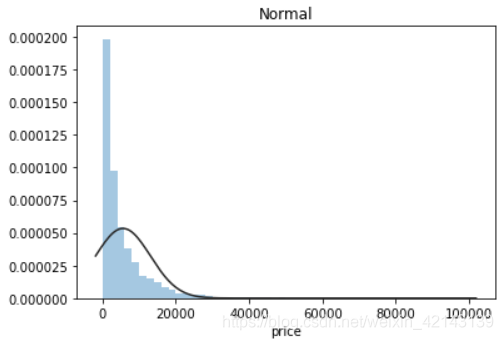
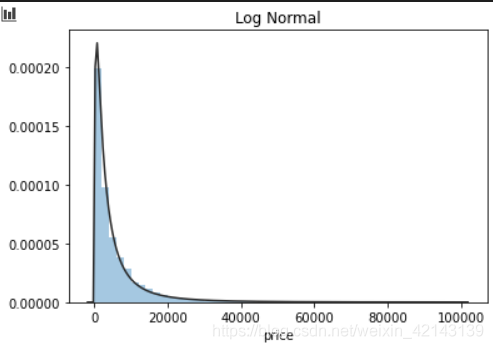
结论:price不服从正态分布,因此在进行回归之前,它必须进行转换。无界约翰逊分布拟合效果较好。 1.2.1.1 相关性分析1.2.1.2 *偏度和峰值偏度(skewness),统计数据分布偏斜方向和程度,是统计数据分布非对称程度的数字特征。定义上偏度是样本的三阶标准化矩。 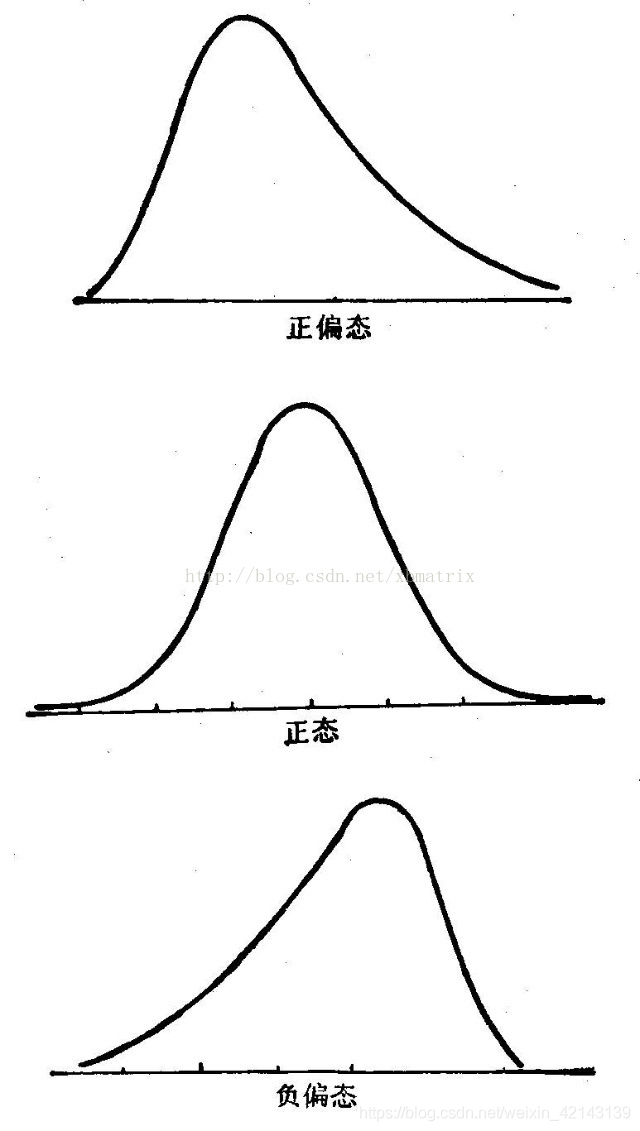
峰度(peakedness;kurtosis)又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。 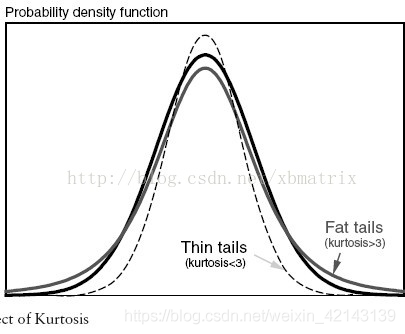
## 2) 查看skewness and kurtosissns.distplot(Train_data['price']);print("Skewness: %f" % Train_data['price'].skew())print("Kurtosis: %f" % Train_data['price'].kurt())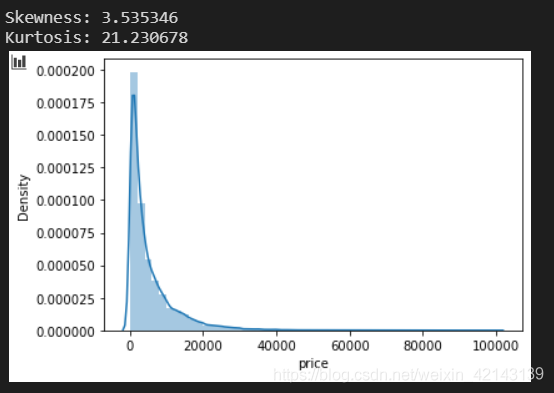
批量计算skew 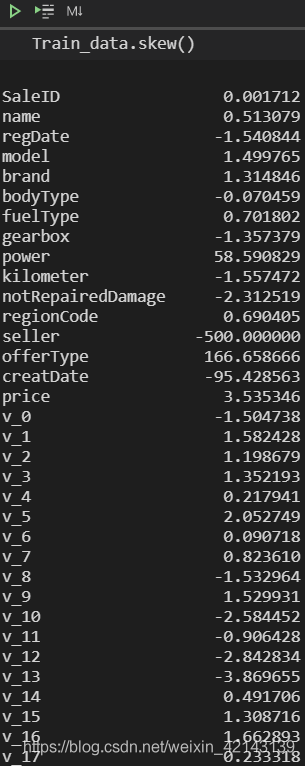
查看skew的分布情况 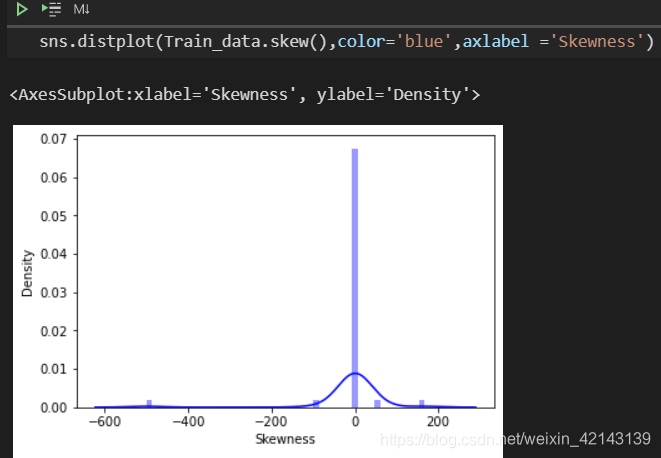
批量计算kurt 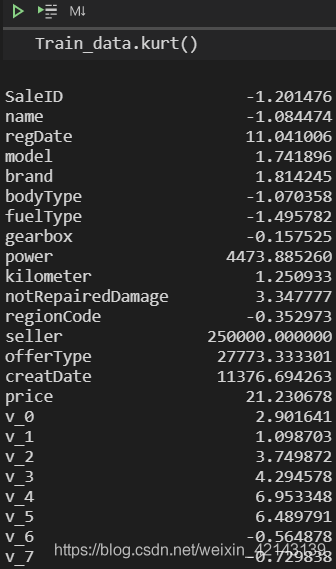
查看kurt的分布情况 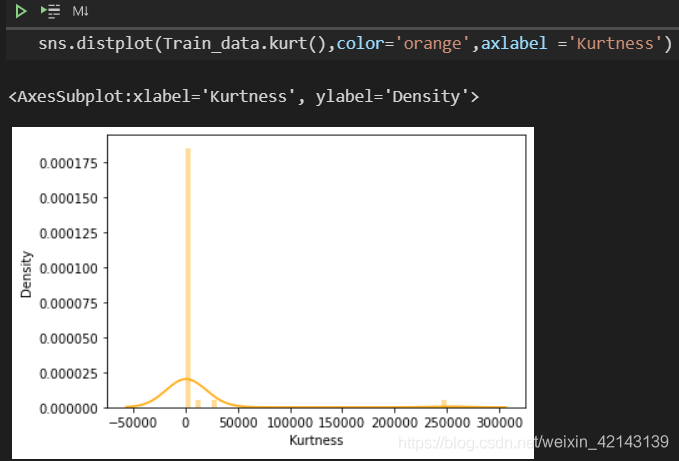
查看目标变量的分布 ## 3) 查看预测值的具体频数plt.hist(Train_data['price'], orientation = 'vertical',histtype = 'bar', color ='red')plt.show() 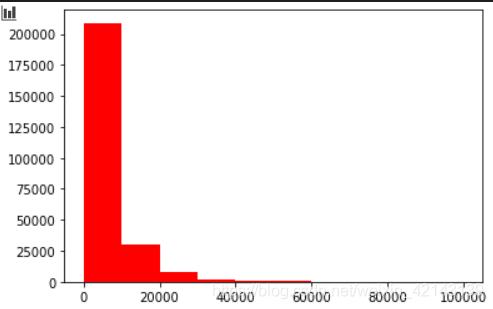
结论:大于20000得值极少,其实这里也可以把这些当作特殊得值(异常值)直接用填充或者删掉 由于np.log(0)==-inf,无法绘图,因此改用log(1+x)绘制分布bar,和教程里有出入,教程里用log绘图如下:(我画不出来,因为-inf会报错) 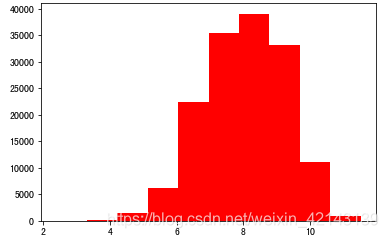
# log变换之后的分布较均匀,可以进行log变换进行预测,这也是预测问题常用的trickplt.hist(np.log(1+Train_data['price']), orientation = 'vertical',histtype = 'bar', color ='red') plt.show() 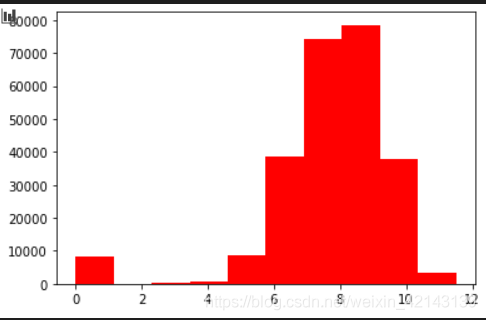
分离label即预测值
Y_train = Train_data['price'] #这个区别方式适用于没有直接label coding的数据 #这里不适用,需要人为根据实际含义来区分 #数字特征 numeric_features = Train_data.select_dtypes(include=[np.number]) numeric_features.columns #类型特征 categorical_features = Train_data.select_dtypes(include=[np.object]) categorical_features.columns
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',] # 特征nunique分布for cat_fea in categorical_features: print(cat_fea + "的特征分布如下:") print("{}特征有个{}不同的值".format(cat_fea, Train_data[cat_fea].nunique())) print(Train_data[cat_fea].value_counts())每个特征情况都会逐个如下所示: 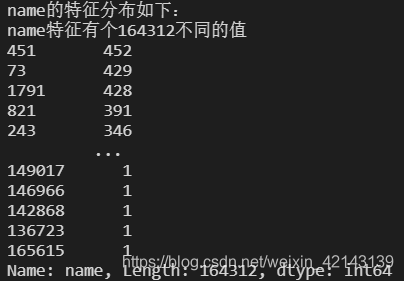
test data显示同理 numeric_features.append('price')numeric_features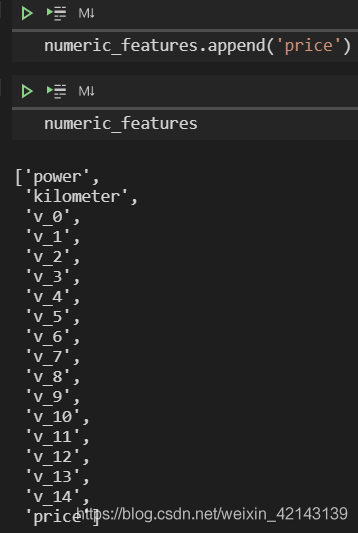
price_numeric = Train_data[numeric_features]correlation = price_numeric.corr()correlation 只截了一部分 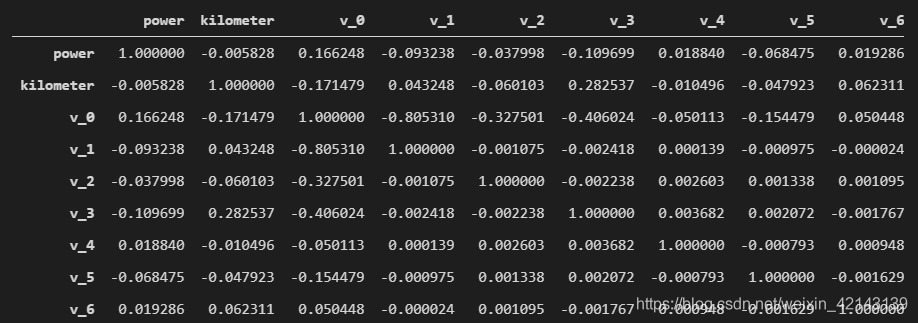
查看相关性(强->弱) print(correlation['price'].sort_values(ascending = False),'/n') 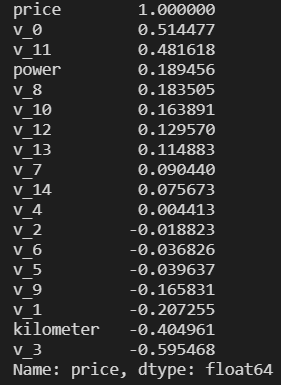
可视化correction f , ax = plt.subplots(figsize = (7, 7))plt.title('Correlation of Numeric Features with Price',y=1,size=16)sns.heatmap(correlation,square = True, vmax=0.8)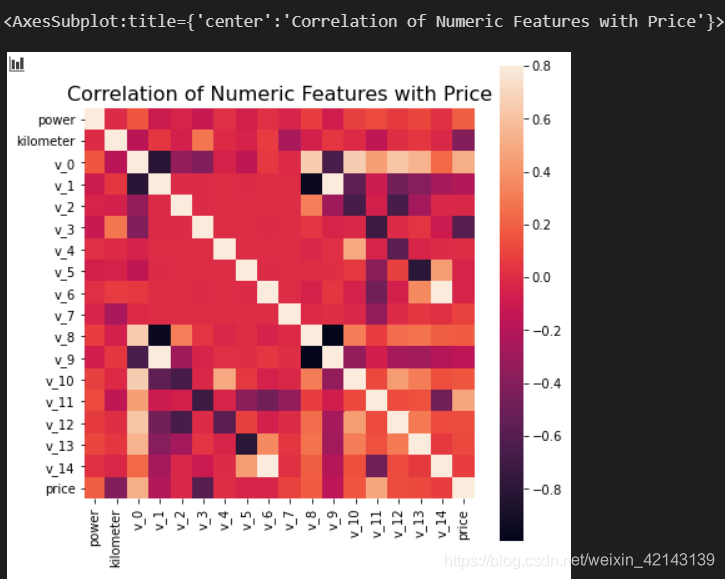
price完成历史使命,删掉 del price_numeric['price'] ## 2) 查看几个特征得 偏度和峰值for col in numeric_features: print('{:15}'.format(col), 'Skewness: {:05.2f}'.format(Train_data[col].skew()) , ' ' , 'Kurtosis: {:06.2f}'.format(Train_data[col].kurt()) )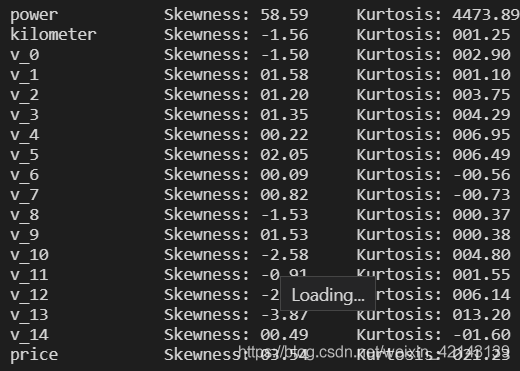
1.2.1.3 *每个数字特征的分布可视化(易忽略)## 3) 每个数字特征得分布可视化f = pd.melt(Train_data, value_vars=numeric_features)g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)g = g.map(sns.distplot, "value") 只截了部分: 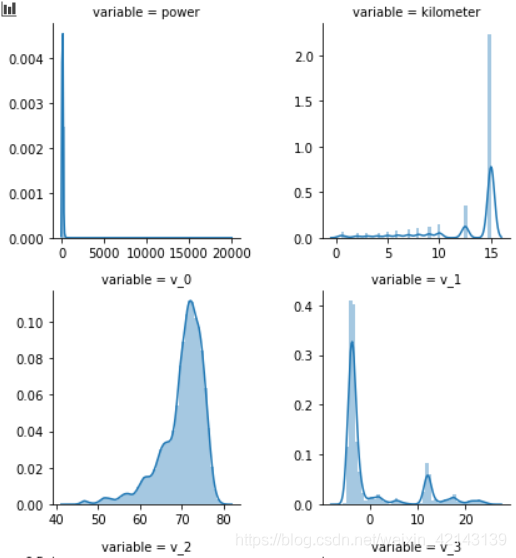
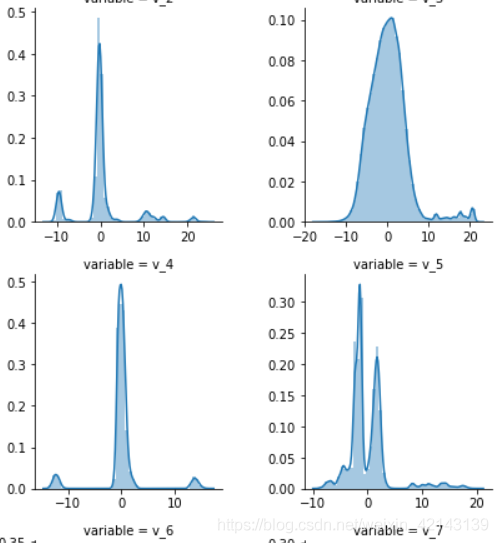
结论:匿名特征(v_*)相对分布均匀
1.2.1.4 *数字特征相互之间的关系可视化(易忽略)## 4) 数字特征相互之间的关系可视化sns.set()columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')plt.show() 1.2.1.5 *多变量互相回归关系可视化(易忽略)## 5) 多变量互相回归关系可视化fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))# ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)
1.2.2 类别特征分析(会画,不会利用结果)对类别特征查看unique分布 ## 1) unique分布for fea in categorical_features: print(Train_data[fea].nunique())categorical_features 1.2.2.1 箱形图可视化## 2) 类别特征箱形图可视化# 因为 name和 regionCode的类别太稀疏了,这里我们把不稀疏的几类画一下categorical_features = ['model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage']for c in categorical_features: Train_data[c] = Train_data[c].astype('category') if Train_data[c].isnull().any(): Train_data[c] = Train_data[c].cat.add_categories(['MISSING']) Train_data[c] = Train_data[c].fillna('MISSING')def boxplot(x, y, **kwargs): sns.boxplot(x=x, y=y) x=plt.xticks(rotation=90)f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)g = g.map(boxplot, "value", "price")1.2.2.2 小提琴图可视化## 3) 类别特征的小提琴图可视化catg_list = categorical_featurestarget = 'price'for catg in catg_list : sns.violinplot(x=catg, y=target, data=Train_data) plt.show() categorical_features = ['model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage'] 1.2.2.3 柱形图可视化类别 ## 4) 类别特征的柱形图可视化def bar_plot(x, y, **kwargs): sns.barplot(x=x, y=y) x=plt.xticks(rotation=90)f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)g = g.map(bar_plot, "value", "price") 1.2.2.4 特征的每个类别频数可视化(count_plot) ## 5) 类别特征的每个类别频数可视化(count_plot)def count_plot(x, **kwargs): sns.countplot(x=x) x=plt.xticks(rotation=90)f = pd.melt(Train_data, value_vars=categorical_features)g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)g = g.map(count_plot, "value")
2. *用pandas_profiling生成数据报告(新技能)pfr = pandas_profiling.ProfileReport(Train_data)pfr.to_file("./example.html")
3. 小结本次笔记虽然针对样本量较少的情况,但仍有一些可贵的思路: a. 通过检查nan缺失情况,确定需要进一步处理的特征: 填充(填充方式是什么,均值填充,0填充,众数填充等); 舍去; 先做样本分类用不同的特征模型去预测。 b. 通过分布,进行异常检测 分析特征异常的label是否异常(或者偏离均值较远或者事特殊符号); 异常值是否应该剔除,还是用正常值填充,等。 c. 通过对laebl作图,分析标签的分布情况 d. 通过对特征作图,特征和label联合做图(统计图,离散图),直观了解特征的分布情况,通过这一步也可以发现数据之中的一些异常值等,通过箱型图分析一些特征值的偏离情况,对于特征和特征联合作图,对于特征和label联合作图,分析其中的一些关联性 到此这篇关于Datawhale练习的文章就介绍到这了,更多相关python预测内容请搜索51zixue.net以前的文章或继续浏览下面的相关文章,希望大家以后多多支持51zixue.net!
python Pool常用函数用法总结
python基础之装饰器详解 |

