自学教程：python的广播机制详解

为什么会有广播机制

python语言在设计的时候，就就考虑到用于两个运算的矩阵或向量维度不匹配的问题。例如，我们有矩阵A，让矩阵每个元素都加1，直接使用
A+1，就可以完成目的。这其中就用到了python的广播机制，所以在很多python的第三方库中，都支持广播机制，例如Numpy、pytorch。

在矩阵或向量相关运算中的广播机制

1、一般的运算

假设我们有一个矩阵A，一个矩阵B，它们的 + - * 运算，就是一一对应元素的操作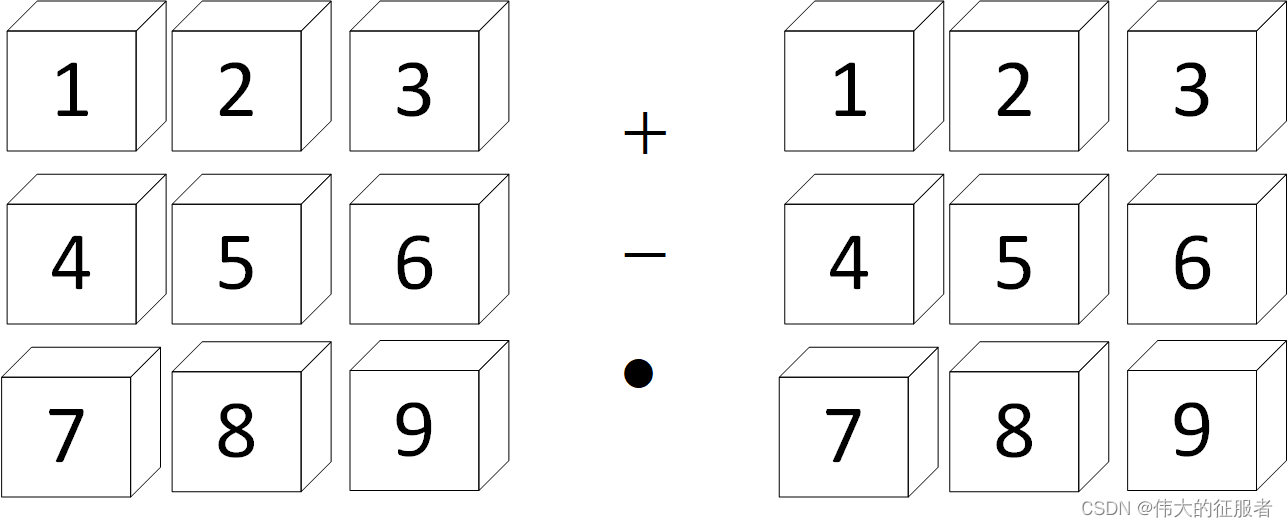

2、一个矩阵一个向量的情况

矩阵 A ∈ R 3 × 3 A/in R^{3/times 3} A∈R3×3 与向量 b ∈ R 1 × 3 b/in R^{1/times 3} b∈R1×3 的运算，向量 b ∈ R 1 × 3 b/in R^{1/times 3} b∈R1×3会根据矩阵A的维度，扩展自身的维度， [ 1 × 3 ] → [ 3 × 3 ] [1/times 3]/to[3 /times 3] [1×3]→[3×3]， 第一个维度大小是1，所以就会向列的方向扩展，即复制多个行。如图所示。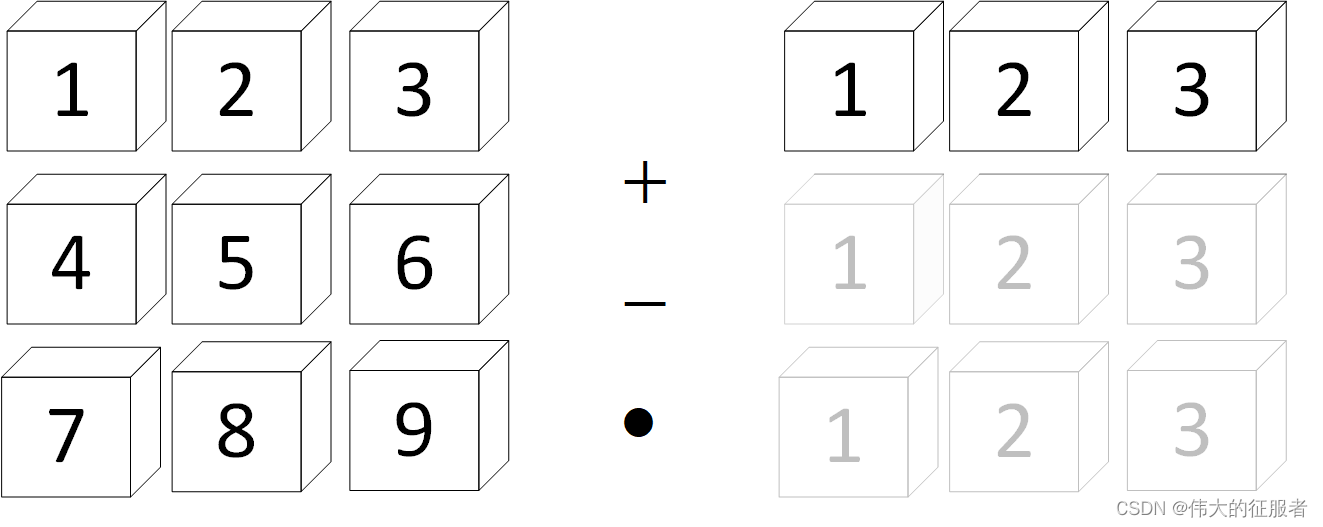

同样，如果向量 b ∈ R 3 × 1 b/in R^{3/times 1} b∈R3×1 ，就会向行扩展，即复制多个列。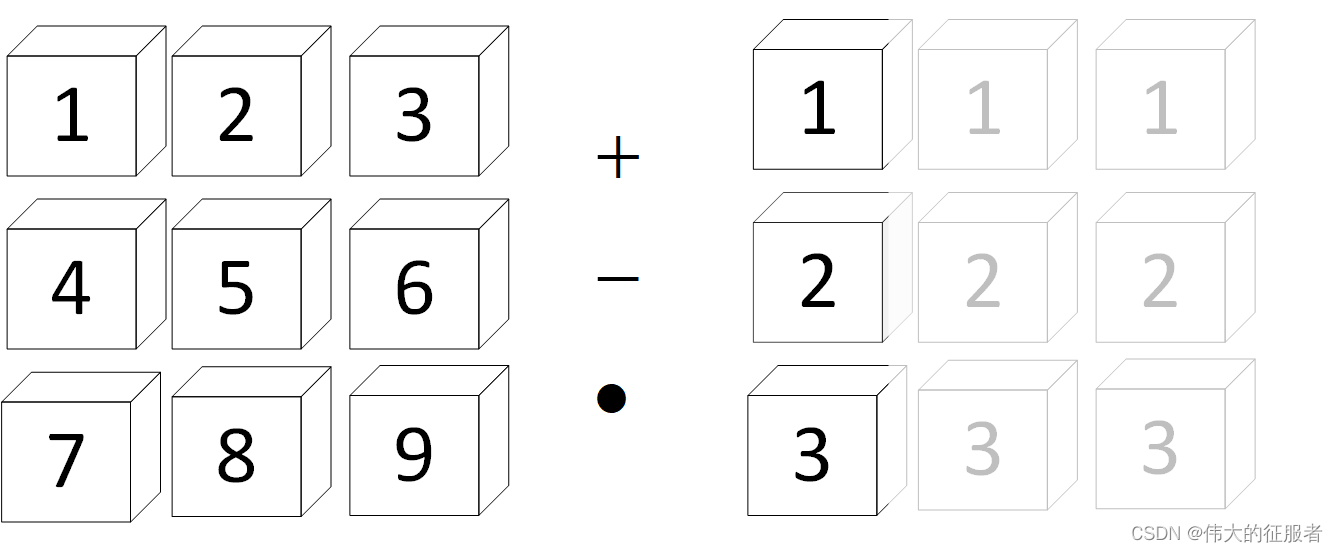

3、两个向量

如果两个向量的size相同，那就没话说了，运算之后也还是向量，只有在两个向量size不相同的时候才有广播。
向量 a ∈ R 3 × 1 a/in R^{3/times 1} a∈R3×1 向量 b ∈ R 1 × 3 b/in R^{1/times 3} b∈R1×3 或者向量 b ∈ R 3 b/in R^{3} b∈R3，两者的size就不一样了。向量a会向维度大小为1的方向扩张，b也是这样。
值得注意的是，我们使用numpy的时候，

# 构造一个向量 import numpy as npa = np.arange(10)  # (10,None)	

a是只有一个维度的。不管你是旋转还是转置，它都不会变化。要想实现广播，就要给a增加一个维度

import numpy as npa = np.arange(10)a = np.expand_dims(a,1)  # (10,1)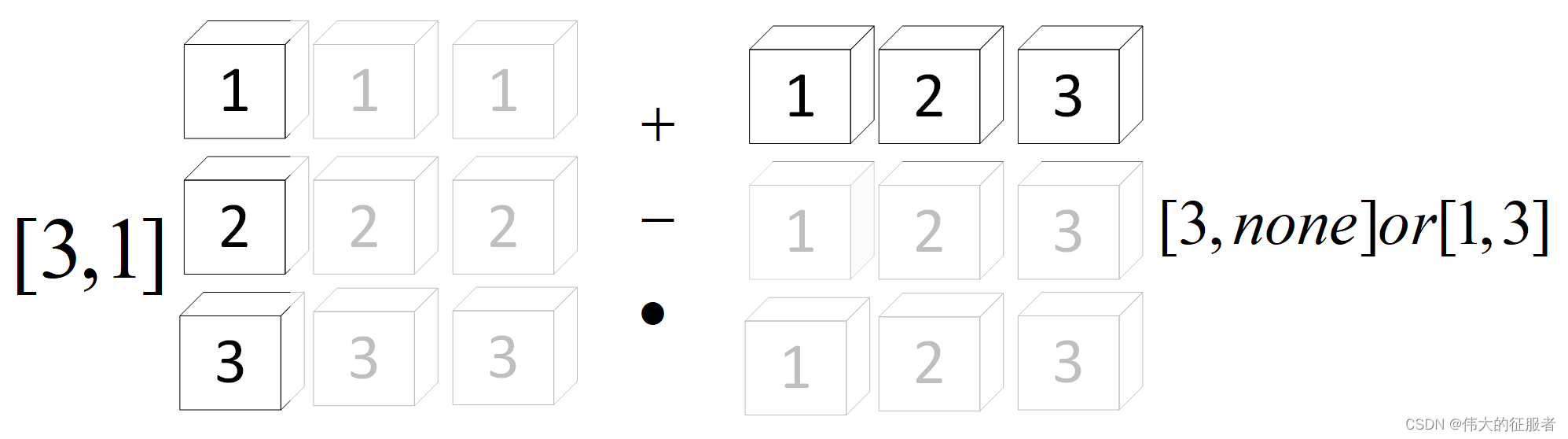

4、矩阵乘法的广播机制

总结

到此这篇关于python的广播机制详解的文章就介绍到这了,更多相关python广播机制内容请搜索51zixue.net以前的文章或继续浏览下面的相关文章希望大家以后多多支持51zixue.net！